Inference for unknown mean and known variance
For a sampling model \(Y|\mu, \sigma^2 \stackrel{iid}{\sim} N(\mu,\sigma^2)\) we wish to make inference on \(\mu\) assuming \(\sigma^2\) is known. The first step will be to derive an expression for \(\pi(\mu|Y=y,\sigma^2)\) which is proportional to \(\pi(\mu|\sigma^2)\pi(y|\mu,\sigma^2)\). To following prior structure will be adopted:
\[Y|\mu,\sigma^2 \sim N(\mu,\sigma^2)\]
\[\mu \sim N(\mu_0,\sigma_0^2)\]
Now we can derive an expression for \(\pi(\mu|Y=y,\sigma^2) \propto \pi(\mu|\sigma^2)\pi(y|\mu,\sigma^2)\).
\[\pi(\mu|\sigma^2)\pi(y|\mu,\sigma^2) \propto e^{-\frac{1}{2\sigma_0^2}(\mu-\mu_o)^2} e^{-\frac{1}{2\sigma^2} (y-\mu)^2}\]
\[= e^{\frac{1}{2}(\frac{1}{\sigma_0^2} (\mu^2-2\mu \mu_0 + \mu_0^2)+\frac{1}{\sigma^2}(y^2-2\mu y+\mu^2))}\]
Now let’s just work with the \(\frac{1}{\sigma_0^2} (\mu^2-2\mu \mu_0 + \mu_0^2)+\frac{1}{\sigma^2}(y^2-2\mu y+\mu^2)\) by itself.
\[\frac{1}{\sigma_0^2} (\mu^2-2\mu \mu_0 + \mu_0^2)+\frac{1}{\sigma^2}(y^2-2\mu y+\mu^2)= \frac{\mu^2}{\sigma^2_0}-\frac{2\mu \mu_0}{\sigma^2_0} + \frac{\mu_0^2}{\sigma_0^2} + \frac{y^2}{\sigma^2} - \frac{2\mu y}{\sigma^2} + \frac{\mu^2}{\sigma^2}\]
\[= \mu^2(\frac{1}{\sigma^2_0} + \frac{1}{\sigma^2}) - 2\mu(\frac{\mu_0}{\sigma_0^2} + \frac{y}{\sigma^2}) + \frac{\mu_0^2}{\sigma_0^2} + \frac{y^2}{\sigma^2}\]
To get this final expression into a quadratic form we can let \(a = \frac{1}{\sigma^2_0} + \frac{1}{\sigma^2}\), \(b = \frac{\mu_0}{\sigma_0^2} + \frac{y}{\sigma^2}\), and \(c = \frac{\mu_0^2}{\sigma_0^2} + \frac{y^2}{\sigma^2}\). In proportionality the \(c\) term will drop from the exponent. Now we have
\[\pi(\mu | \sigma^2,y) \propto e^{-\frac{1}{2}(a\mu^2-2b\mu)} = e^{-\frac{1}{2}a(\mu^2 - 2b\mu/a+b^2/a^2)+b^2/2a}\]
\[= e^{-\frac{1}{2}a(\mu - b/a)^2} = e^{-\frac{1}{2}(\frac{\mu-b/a}{1/\sqrt{a}})^2}\]
Which is recognizable as the kernel of a \(N(b/a,1/a) = N(\mu_n = \frac{\frac{\mu_0}{\sigma_0^2} + \frac{y}{\sigma^2}}{\frac{1}{\sigma^2_0} + \frac{1}{\sigma^2}}, \sigma^2_n = \frac{1}{\frac{1}{\sigma^2_0} + \frac{1}{\sigma^2}})\).
Inference for unknown mean and unknown variance
It is more reasonable to expect that in an actual data analysis if we are trying to estimate the mean of a normal population then we likely need to estimate the variance as well. The following parameterization is used by Hoff in A First Course in Bayesian Statistical Methods.
\[1/\sigma^2 \sim gamma(shape = \frac{\nu_0}{2},rate = \frac{\nu_0 \sigma^2_0}{2})\]
\[\mu|\sigma^2 \sim N(\mu_0,\frac{\sigma^2}{\kappa_0})\]
\[Y_1,...,Y_n|\mu,\sigma^2 \stackrel{iid}{\sim} N(\mu,\sigma^2)\]
The posterior joint distribution of \(\mu,\sigma^2\) after observing the data \(Y_1,...,Y_n\) is given by the following product.
\[\pi(\mu,\sigma^2|y_1,...,y_n) = \pi(\mu|\sigma^2,y_1,...,y_n)\pi(\sigma^2|y_1,...,y_n)\]
This first term \(\pi(\mu|\sigma^2,y_1,...,y_n)\) is the conditional posterior distribution of \(\mu\). Since it is conditional on \(\sigma^2\) (i.e. \(\sigma^2\) is “known”) it can be derived with a calculation identical to the one given in the previous section. Generalizing to a sample of size \(n\) instead of size 1 and substituting \(\sigma^2/\kappa_n\) for \(\sigma^2_0\) we get that
\[\mu|y_1,...,y_n,\sigma^2 \sim N(\mu_n = \frac{\kappa_0 \mu_0 + n\bar{y}}{\kappa_n},\frac{\sigma^2}{\kappa_n})\]
where \(\kappa_n = \kappa_0 + n\). Hoff’s parameterization lends itself to a nice interpretation of \(\mu_0\) and the mean of \(\kappa_0\) prior observations and \(\mu_n\) as the mean of \(\kappa_0\) prior observations and \(n\) new observations all together. Also, the variance of \(\mu|y_1,...,y_n,\sigma^2\) is \(\sigma^2/\kappa_n\).
Now to get the posterior distribution of \(\sigma^2\) after observing \(y_1,...,y_n\) we need to integrate over all possible values of \(\mu\) according to
\[\pi(\sigma^2|y_1,...,y_n) \propto \pi(\sigma^2) \pi(y_1,...,y_n|\sigma^2)\]
\[= \pi(\sigma^2) \int_\mu \pi(y_1,...,y_n|\mu,\sigma^2)\pi(\mu|\sigma^2) d\mu\]
\[= \pi(\sigma^2) \int_\mu (\frac{1}{2\pi \sigma^2})^{-n/2} e^{-\frac{\sum(y_i-\mu)^2}{2\sigma^2}} (\frac{1}{2\pi \sigma^2/\kappa_0})^{-1/2} e^{-\frac{(\mu-\mu_0)^2}{2\sigma^2/\kappa_0}}d\mu\]
Eventually, we get that \(\sigma^2|y_1,...,y_n \sim IG(\nu_n/2,\nu_n \sigma^2_n/2)\) or alternatively \(1/\sigma^2|y_1,...,y_n \sim Gamma(\nu_n/2,\nu_n\sigma^2_n/2)\), where
\[\nu_n = \nu_0 + n\]
\[\sigma^2_n = \frac{1}{\nu_n}[\nu_0 \sigma^2_0 + (n-1)s^2+\frac{\kappa_0n}{\kappa_n}(\bar{y}-\mu_0)^2]\]
We get another nice interpretation here of \(\nu_0\) as the prior sample size with corresponding sample variance \(\sigma^2_0\). Also \(s^2\) is the sample variance and \((n-1)s^2\) is the sample sum of squares.
normR
# devtools::install_github("carter-allen/normR")
library(normR)Monte Carlo Sampling
Example from Hoff pg. 76.
# parameters for the normal prior
mu_0 <- 1.9
kappa_0 <- 1
# parameters for the gamma prior
sigsq_0 <- 0.010
nu_0 <- 1
# some data
ys <- c(1.64,1.70,1.72,1.74,1.82,1.82,1.82,1.90,2.08)
n <- length(ys)
y_bar <- mean(ys)
ssq <- var(ys)
# posterior parameters
kappa_n <- kappa_0 + n
nu_n <- nu_0 + n
mu_n <- mu_n(kappa_0,mu_0,n,y_bar)
sigsq_n <- sigsq_n(nu_0,sigsq_0,n,ssq,kappa_0,y_bar,mu_0)mu_n## [1] 1.814sigsq_n## [1] 0.015324# posterior variance draws
sigsq_posterior_draw <- draw_sigsq_posterior(10000,nu_n,sigsq_n)
# posterior mean draws
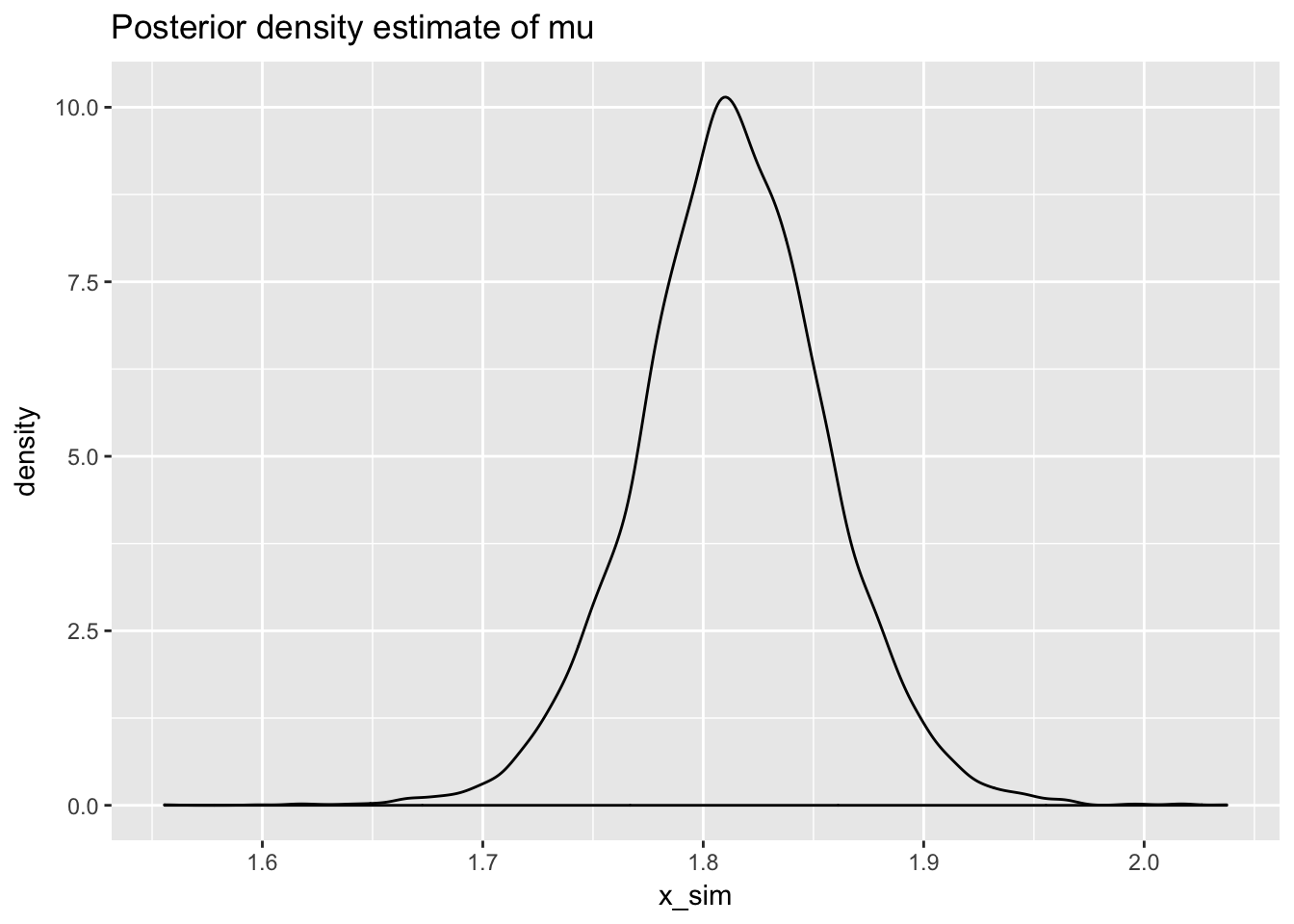
mu_posterior_draw <- draw_mu_posterior(mu_n,sigsq_posterior_draw,kappa_n)quantile(mu_posterior_draw,c(0.025,0.975))## 2.5% 97.5%
## 1.727323 1.899154# plot posterior draws
normR::plot_monte_sim(sigsq_posterior_draw,mu_posterior_draw)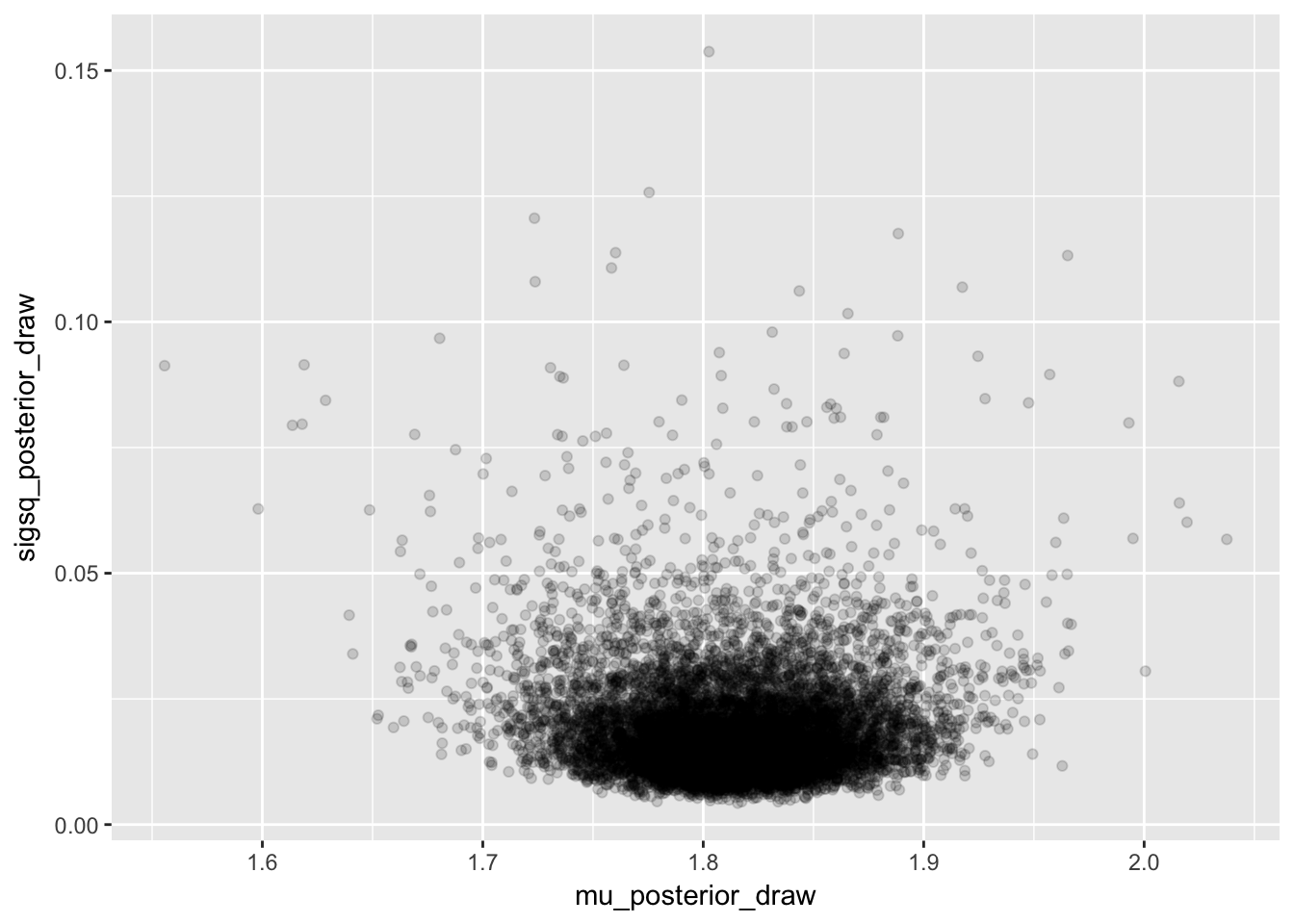
# plot posterior density estimate for sigma
normR::plot_posterior_density_estimate(sigsq_posterior_draw,
plot_title = "Posterior density estimate of sigma")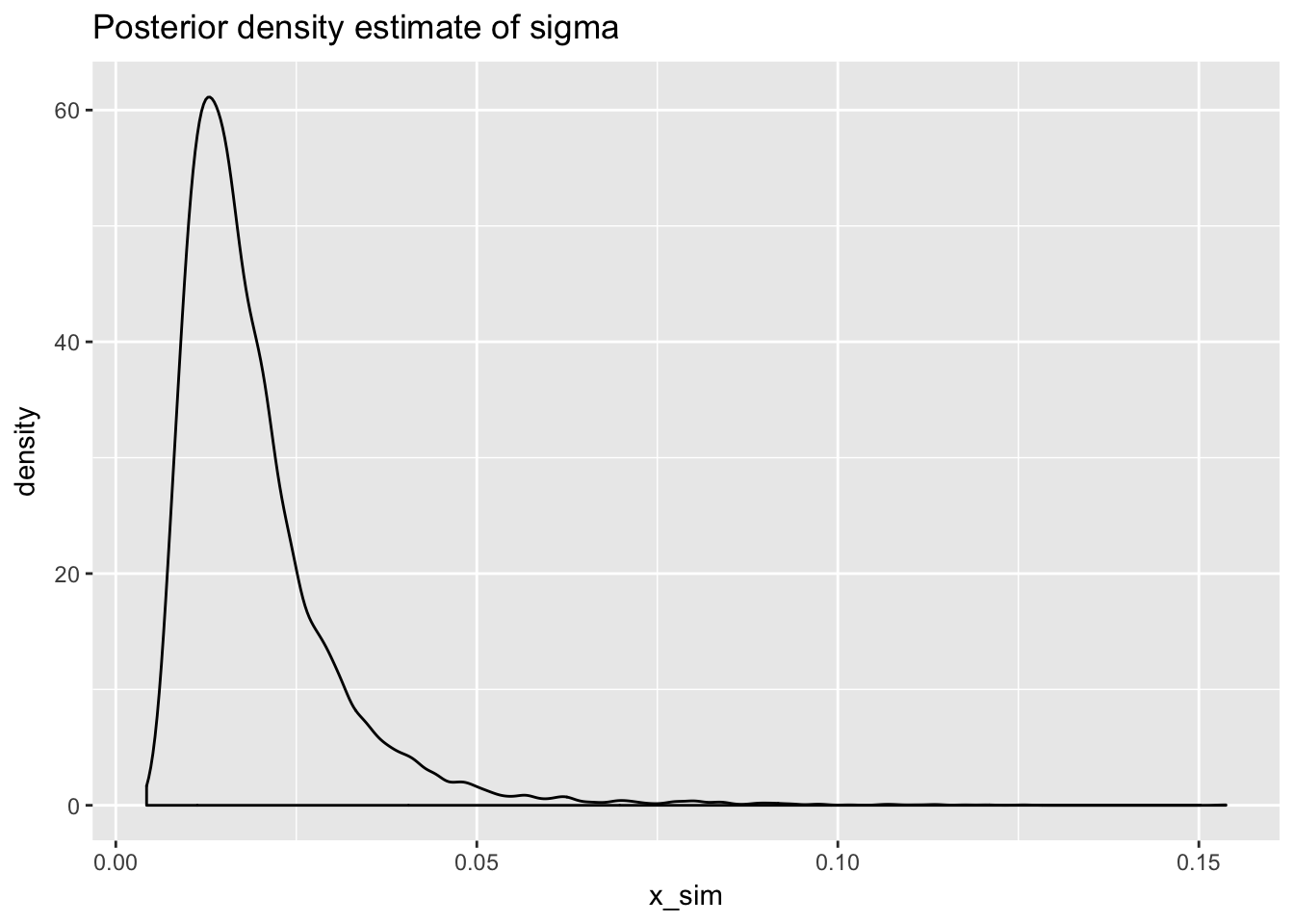
# posterior density estimate of mu
normR::plot_posterior_density_estimate(mu_posterior_draw,
plot_title = "Posterior density estimate of mu")